Elastic modulus

An elastic modulus, or modulus of elasticity, is the mathematical description of an object or substance's tendency to be deformed elastically (i.e., non-permanently) when a force is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region:^[1] As such, a stiffer material will have a higher elastic modulus.

$\lambda \ \stackrel{\text{def}}{=}\ \frac {\text{stress}} {\text{strain}}$

where lambda (λ) is the elastic modulus; stress is the restoring force caused due to the deformation divided by the area to which the force is applied; and strain is the ratio of the change caused by the stress to the original state of the object. If stress is measured in pascals, since strain is a dimensionless quantity, then the units of λ are pascals as well.^[2]

Since the denominator becomes unity if length is doubled, the elastic modulus becomes the stress induced in the material,when the sample of the material turns double of its original length on applying external force. While this endpoint is not realistic because most materials will fail before reaching it, it is practical, in that small fractions of the defining load will operate in exactly the same ratio. Thus, for steel with a Young's modulus of 30 million psi, a 30 thousand psi load will elongate a 1 inch bar by one thousandth of an inch; similarly, for metric units, where a thousandth of the modulus in gigapascals will change a meter by a millimeter.

Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are:

Young's modulus (E) describes tensile elasticity, or the tendency of an object to deform along an axis when opposing forces are applied along that axis; it is defined as the ratio of tensile stress to tensile strain. It is often referred to simply as the elastic modulus.
The shear modulus or modulus of rigidity (G or 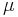$\mu \,$ ) describes an object's tendency to shear (the deformation of shape at constant volume) when acted upon by opposing forces; it is defined as shear stress over shear strain. The shear modulus is part of the derivation of viscosity.
The bulk modulus (K) describes volumetric elasticity, or the tendency of an object to deform in all directions when uniformly loaded in all directions; it is defined as volumetric stress over volumetric strain, and is the inverse of compressibility. The bulk modulus is an extension of Young's modulus to three dimensions.

Three other elastic moduli are Poisson's ratio, Lamé's first parameter, and P-wave modulus.

Homogeneous and isotropic (similar in all directions) materials (solids) have their (linear) elastic properties fully described by two elastic moduli, and one may choose any pair. Given a pair of elastic moduli, all other elastic moduli can be calculated according to formulas in the table below at the end of page.

Inviscid fluids are special in that they cannot support shear stress, meaning that the shear modulus is always zero. This also implies that Young's modulus is always zero.

References

^ Askeland, Donald R.; Phulé, Pradeep P. (2006). The science and engineering of materials (5th ed.). Cengage Learning. p. 198. ISBN 978-0-53-455396-8. http://books.google.com/books?id=fRbZslUtpBYC&pg=PA198.
^ Beer, Ferdinand P.; Johnston, E. Russell; Dewolf, John; Mazurek, David (2009). Mechanics of Materials. McGraw Hill. p. 56. ISBN 978-0-07-015389-9.

Conversion formulas
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these, thus given any two, any other of the elastic moduli can be calculated according to these formulas.
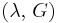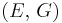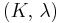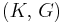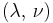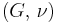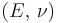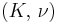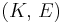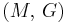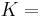	$(\lambda,\,G)$	$(E,\,G)$	$(K,\,\lambda)$	$(K,\,G)$	$(\lambda,\,\nu)$	$(G,\,\nu)$	$(E,\,\nu)$	$(K,\, \nu)$	$(K,\,E)$	$(M,\,G)$
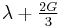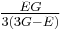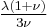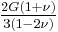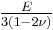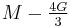$K=\,$	$\lambda%2B \tfrac{2G}{3}$	$\tfrac{EG}{3(3G-E)}$			$\tfrac{\lambda(1%2B\nu)}{3\nu}$	$\tfrac{2G(1%2B\nu)}{3(1-2\nu)}$	$\tfrac{E}{3(1-2\nu)}$			$M - \tfrac{4G}{3}$
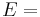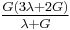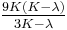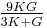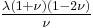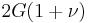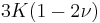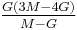$E=\,$	$\tfrac{G(3\lambda %2B 2G)}{\lambda %2B G}$		$\tfrac{9K(K-\lambda)}{3K-\lambda}$	$\tfrac{9KG}{3K%2BG}$	$\tfrac{\lambda(1%2B\nu)(1-2\nu)}{\nu}$	$2G(1%2B\nu)\,$		$3K(1-2\nu)\,$		$\tfrac{G(3M-4G)}{M-G}$
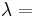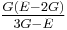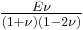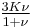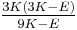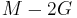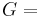$\lambda=\,$		$\tfrac{G(E-2G)}{3G-E}$		$K-\tfrac{2G}{3}$		$\tfrac{2 G \nu}{1-2\nu}$	$\tfrac{E\nu}{(1%2B\nu)(1-2\nu)}$	$\tfrac{3K\nu}{1%2B\nu}$	$\tfrac{3K(3K-E)}{9K-E}$	$M - 2G\,$
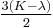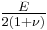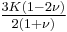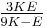$G=\,$			$\tfrac{3(K-\lambda)}{2}$		$\tfrac{\lambda(1-2\nu)}{2\nu}$		$\tfrac{E}{2(1%2B\nu)}$	$\tfrac{3K(1-2\nu)}{2(1%2B\nu)}$	$\tfrac{3KE}{9K-E}$
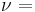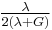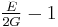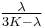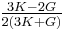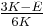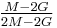$\nu=\,$	$\tfrac{\lambda}{2(\lambda %2B G)}$	$\tfrac{E}{2G}-1$	$\tfrac{\lambda}{3K-\lambda}$	$\tfrac{3K-2G}{2(3K%2BG)}$					$\tfrac{3K-E}{6K}$	$\tfrac{M - 2G}{2M - 2G}$
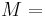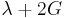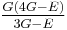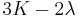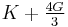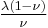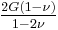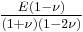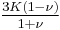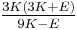$M=\,$	$\lambda%2B2G\,$	$\tfrac{G(4G-E)}{3G-E}$	$3K-2\lambda\,$	$K%2B\tfrac{4G}{3}$	$\tfrac{\lambda(1-\nu)}{\nu}$	$\tfrac{2G(1-\nu)}{1-2\nu}$	$\tfrac{E(1-\nu)}{(1%2B\nu)(1-2\nu)}$	$\tfrac{3K(1-\nu)}{1%2B\nu}$	$\tfrac{3K(3K%2BE)}{9K-E}$

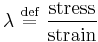
Elastic modulus

See also

References

Further reading